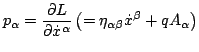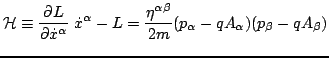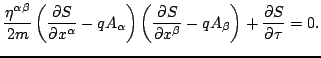


Next: Solution to the Hamilton-Jacobi
Up: Laser-driven particle mechanics
Previous: The Dynamical Phase
Contents
Being defined in terms of the action integral, the dynamical phase
satisfies a differential equation which one obtains by a simple
argument:
Let
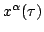 and
and
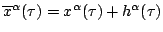 be two
worldlines having the same starting point
be two
worldlines having the same starting point
both satisfying Lagrange's equation of motion, but having slightly
different termination points
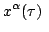 and and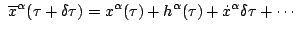 |
|
as in Figure 4. Then the (principal linear part of the) difference in
the value of the dynamical phase at these termination points is
Figure 4:
Differential of the action
function 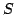 as a function of variations
as a function of variations
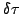 and
and
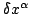 in the endpoint of an extremal world line.
in the endpoint of an extremal world line.
![\includegraphics[scale=.75]{action_differential.eps}](img87.png) |
The fact that
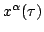 satisfies Lagrange's equation of motion
implies that the integral vanishes. Recalling the definition of
satisfies Lagrange's equation of motion
implies that the integral vanishes. Recalling the definition of
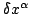 , or looking at Figure 4, one
sees that at the two termination points one has
, or looking at Figure 4, one
sees that at the two termination points one has
Consequently, the principal linear part of the difference between the
two  values at the termination point is
values at the termination point is
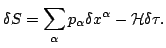 |
(10) |
Here
are the momentum components and
is the superhamiltonian of the charged particle at the termination
point of its worldline. Equation (11) is the expression for
the differential of  . One has
. One has
Thus the differential equation for the dynamical phase function 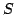 is
is
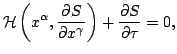 |
(11) |
or explicitly
This is the Hamilton-Jacobi for a charged particle in an
electromagnetic vector potential
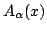 .
.



Next: Solution to the Hamilton-Jacobi
Up: Laser-driven particle mechanics
Previous: The Dynamical Phase
Contents
Ulrich Gerlach
2005-11-07
![]() and
and
![]() be two
worldlines having the same starting point
be two
worldlines having the same starting point
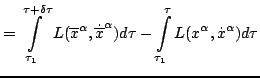
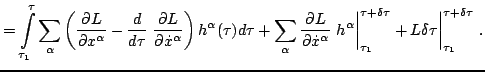
![\includegraphics[scale=.75]{action_differential.eps}](img87.png)
![]() satisfies Lagrange's equation of motion
implies that the integral vanishes. Recalling the definition of
satisfies Lagrange's equation of motion
implies that the integral vanishes. Recalling the definition of
![]() , or looking at Figure 4, one
sees that at the two termination points one has
, or looking at Figure 4, one
sees that at the two termination points one has